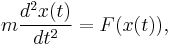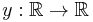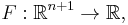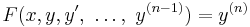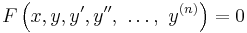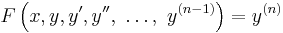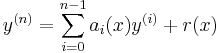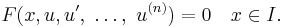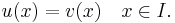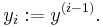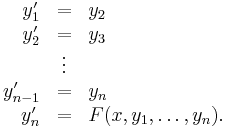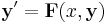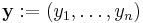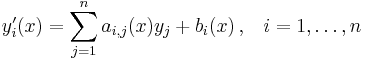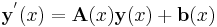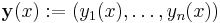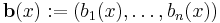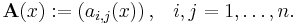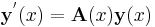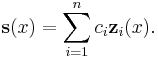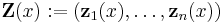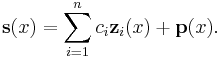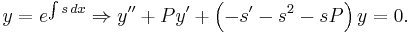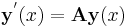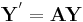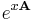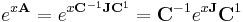Ordinary differential equation

In mathematics, an ordinary differential equation (or ODE) is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable.

A simple example is Newton's second law of motion, which leads to the differential equation

$m \frac{d^2 x(t)}{dt^2} = F(x(t)),\,$

for the motion of a particle of constant mass m. In general, the force F depends upon the position x(t) of the particle at time t, and thus the unknown function x(t) appears on both sides of the differential equation, as is indicated in the notation F(x(t)).

Ordinary differential equations are distinguished from partial differential equations, which involve partial derivatives of several variables.

Ordinary differential equations arise in many different contexts including geometry, mechanics, astronomy and population modelling. Many famous mathematicians have studied differential equations and contributed to the field, including Newton, Leibniz, the Bernoulli family, Riccati, Clairaut, d'Alembert and Euler.

Much study has been devoted to the solution of ordinary differential equations. In the case where the equation is linear, it can be solved by analytical methods. Unfortunately, most of the interesting differential equations are non-linear and, with a few exceptions, cannot be solved exactly. Approximate solutions are arrived at using computer approximations (see numerical ordinary differential equations).

The trajectory of a projectile launched from a cannon follows a curve determined by an ordinary differential equation that is derived from Newton's second law.

Existence and uniqueness of solutions

There are several theorems that establish existence and uniqueness of solutions to initial value problems involving ODEs both locally and globally. See Picard–Lindelöf theorem for a brief discussion of this issue.

Definitions

Ordinary differential equation

Let y be an unknown function

$y: \mathbb{R} \to \mathbb{R}$

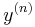in x with $y^{(n)}$ the nth derivative of y, and let F be a given function

$F:\mathbb{R}^{n+1}\rightarrow\mathbb{R},$

then an equation of the form

$F(x,y,y',\ \dots,\ y^{(n-1)})=y^{(n)}$

is called an ordinary differential equation (ODE) of order n. If y is an unknown vector valued function

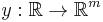$y: \mathbb{R} \to \mathbb{R}^m$ ,

it is called a system of ordinary differential equations of dimension m (in this case, F : ℝ^mn+1→ ℝ^m).

More generally, an implicit ordinary differential equation of order n has the form

$F\left(x, y, y', y'',\ \dots,\ y^{(n)}\right) = 0$

where F : ℝⁿ⁺²→ ℝ depends on y⁽ⁿ⁾. To distinguish the above case from this one, an equation of the form

$F\left(x, y, y', y'',\ \dots,\ y^{(n-1)}\right) = y^{(n)}$

is called an explicit differential equation.

A differential equation not depending on x is called autonomous.

A differential equation is said to be linear if F can be written as a linear combination of the derivatives of y together with a constant term, all possibly depending on x:

$y^{(n)} = \sum_{i=0}^{n-1} a_i(x) y^{(i)} + r(x)$

with a_i(x) and r(x) continuous functions in x. The function r(x) is called the source term; if r(x)=0 then the linear differential equation is called homogeneous, otherwise it is called non-homogeneous or inhomogeneous.

Solutions

Given a differential equation

$F(x, y, y', \dots, y^{(n)}) = 0$

a function u: I ⊂ R → R is called the solution or integral curve for F, if u is n-times differentiable on I, and

$F(x,u,u',\ \dots,\ u^{(n)})=0 \quad x \in I.$

Given two solutions u: J ⊂ R → R and v: I ⊂ R → R, u is called an extension of v if I ⊂ J and

$u(x) = v(x) \quad x \in I.\,$

A solution which has no extension is called a global solution.

A general solution of an n-th order equation is a solution containing n arbitrary variables, corresponding to n constants of integration. A particular solution is derived from the general solution by setting the constants to particular values, often chosen to fulfill set 'initial conditions or boundary conditions'. A singular solution is a solution that can't be derived from the general solution.

Examples

Reduction to a first order system

Any differential equation of order n can be written as a system of n first-order differential equations. Given an explicit ordinary differential equation of order n (and dimension 1),

$F\left(x, y, y', y'',\ \dots,\ y^{(n-1)}\right) = y^{(n)}$

define a new family of unknown functions

$y_i�:= y^{(i-1)}.\!$

for i from 1 to n.

The original differential equation can be rewritten as the system of differential equations with order 1 and dimension n given by

$\begin{array}{rcl} y_1^\prime&=&y_2\\ y_2^\prime&=&y_3\\ &\vdots&\\ y_{n-1}^\prime&=&y_n\\ y_n^\prime&=&F(x,y_1,\dots,y_n). \end{array}$

which can be written concisely in vector notation as

$\mathbf{y}^\prime=\mathbf{F}(x,\mathbf{y})$

with

$\mathbf{y}:=(y_1,\dots,y_n)$

and

$\mathbf{F}(x,y_1,\dots,y_n)=(y_2,\dots,y_n,F(x,y_1,\dots,y_n)).$

Linear ordinary differential equations

A well understood particular class of differential equations is linear differential equations. We can always reduce an explicit linear differential equation of any order to a system of differential equation of order 1

$y_i'(x) = \sum_{j=1}^n a_{i,j}(x) y_j + b_i(x) \, \mathrm{,} \quad i = 1,\ldots,n$

which we can write concisely using matrix and vector notation as

$\mathbf{y}^'(x) = \mathbf{A}(x) \mathbf{y}(x) + \mathbf{b}(x)$

with

$\mathbf{y}(x):=(y_1(x),\ldots,y_n(x))$

$\mathbf{b}(x):=(b_1(x),\ldots,b_n(x))$

$\mathbf{A}(x):=(a_{i,j}(x)) \, \mathrm{,} \quad i,j = 1,\ldots,n.$

Homogeneous equations

The set of solutions for a system of homogeneous linear differential equations of order 1 and dimension n

$\mathbf{y}^'(x) = \mathbf{A}(x) \mathbf{y}(x)$

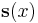forms an n-dimensional vector space. Given a basis for this vector space $\mathbf{z}_1(x), \ldots, \mathbf{z}_n(x)$ , which is called a fundamental system, every solution $\mathbf{s}(x)$ can be written as

$\mathbf{s}(x) = \sum_{i=1}^{n} c_i \mathbf{z}_i(x).$

The n × n matrix

$\mathbf{Z}(x)�:= (\mathbf{z}_1(x), \ldots, \mathbf{z}_n(x))$

is called fundamental matrix. In general there is no method to explicitly construct a fundamental system, but if one solution is known d'Alembert reduction can be used to reduce the dimension of the differential equation by one.

Nonhomogeneous equations

The set of solutions for a system of inhomogeneous linear differential equations of order 1 and dimension n

$\mathbf{y}^'(x) = \mathbf{A}(x) \mathbf{y}(x) + \mathbf{b}(x)$

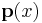can be constructed by finding the fundamental system $\mathbf{z}_1(x), \ldots, \mathbf{z}_n(x)$ to the corresponding homogeneous equation and one particular solution $\mathbf{p}(x)$ to the inhomogeneous equation. Every solution 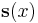$\mathbf{s}(x)$ to nonhomogeneous equation can then be written as

$\mathbf{s}(x) = \sum_{i=1}^{n} c_i \mathbf{z}_i(x) + \mathbf{p}(x).$

A particular solution to the nonhomogeneous equation can be found by the method of undetermined coefficients or the method of variation of parameters.

Concerning second order linear ordinary differential equations, it is well known that

$y = e^{\int s \, dx } \Rightarrow y'' + Py' + \left ( -s' -s^2 -sP \right ) y = 0 .$

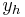So, if $y_h$ is a solution of: 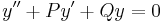$y'' + Py' + Qy = 0$ , then 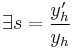$\exists s = {y_h' \over y_h}$ such that: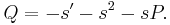 $Q = -s' - s^2 - sP .$

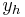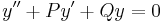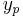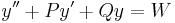So, if $y_h$ is a solution of: $y'' + Py' + Qy = 0$ ; then a particular solution $y_p$ of $y'' + Py' + Qy = W$ , is given by:

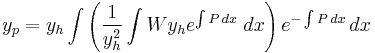$y_p = y_h \int { \left ( { 1 \over y_h^2} \int W y_h e^{\int P \,dx \,} \, dx \right ) e^{- \int P \, dx } \, dx }$ . ^[1]

Fundamental systems for homogeneous equations with constant coefficients

If a system of homogeneous linear differential equations has constant coefficients

$\mathbf{y}^'(x) = \mathbf{A} \mathbf{y}(x)$

then we can explicitly construct a fundamental system. The fundamental system can be written as a matrix differential equation

$\mathbf{Y}^' = \mathbf{A} \mathbf{Y}$

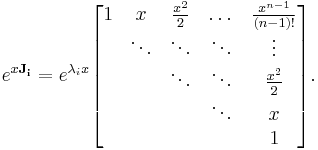
with solution as a matrix exponential

$e^{x \mathbf{A}}$

which is a fundamental matrix for the original differential equation. To explicitly calculate this expression we first transform A into Jordan normal form

$e^{x \mathbf{A}} = e^{x \mathbf{C}^{-1} \mathbf{J} \mathbf{C}^{1}} = \mathbf{C}^{-1} e^{x \mathbf{J}} \mathbf{C}^{1}$

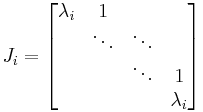
and then evaluate the Jordan blocks

$J_i = \begin{bmatrix} \lambda_i & 1 & \; & \; \\ \; & \ddots & \ddots & \; \\ \; & \; & \ddots & 1 \\ \; & \; & \; & \lambda_i \end{bmatrix}$

of J separately as

$e^{x \mathbf{J_i}} = e^{\lambda_i x} \begin{bmatrix} 1 & x & \frac{x^2}{2} & \dots & \frac{x^{n-1}}{(n-1)!} \\ \; & \ddots & \ddots & \ddots & \vdots \\ \; & \; & \ddots & \ddots & \frac{x^2}{2} \\ \; & \; & \; & \ddots & x \\ \; & \; & \; & \; & 1 \end{bmatrix} .$

Theories of ODEs

Singular solutions

The theory of singular solutions of ordinary and partial differential equations was a subject of research from the time of Leibniz, but only since the middle of the nineteenth century did it receive special attention. A valuable but little-known work on the subject is that of Houtain (1854). Darboux (starting in 1873) was a leader in the theory, and in the geometric interpretation of these solutions he opened a field which was worked by various writers, notably Casorati and Cayley. To the latter is due (1872) the theory of singular solutions of differential equations of the first order as accepted circa 1900.

Reduction to quadratures

The primitive attempt in dealing with differential equations had in view a reduction to quadratures. As it had been the hope of eighteenth-century algebraists to find a method for solving the general equation of the 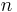$n$ th degree, so it was the hope of analysts to find a general method for integrating any differential equation. Gauss (1799) showed, however, that the differential equation meets its limitations very soon unless complex numbers are introduced. Hence analysts began to substitute the study of functions, thus opening a new and fertile field. Cauchy was the first to appreciate the importance of this view. Thereafter the real question was to be, not whether a solution is possible by means of known functions or their integrals, but whether a given differential equation suffices for the definition of a function of the independent variable or variables, and if so, what are the characteristic properties of this function.

Fuchsian theory

Two memoirs by Fuchs (Crelle, 1866, 1868), inspired a novel approach, subsequently elaborated by Thomé and Frobenius. Collet was a prominent contributor beginning in 1869, although his method for integrating a non-linear system was communicated to Bertrand in 1868. Clebsch (1873) attacked the theory along lines parallel to those followed in his theory of Abelian integrals. As the latter can be classified according to the properties of the fundamental curve which remains unchanged under a rational transformation, so Clebsch proposed to classify the transcendent functions defined by the differential equations according to the invariant properties of the corresponding surfaces f = 0 under rational one-to-one transformations.

Lie's theory

From 1870 Sophus Lie's work put the theory of differential equations on a more satisfactory foundation. He showed that the integration theories of the older mathematicians can, by the introduction of what are now called Lie groups, be referred to a common source; and that ordinary differential equations which admit the same infinitesimal transformations present comparable difficulties of integration. He also emphasized the subject of transformations of contact.

Sturm–Liouville theory

Sturm–Liouville theory is a theory of eigenvalues and eigenfunctions of linear operators defined in terms of second-order homogeneous linear equations, and is useful in the analysis of certain partial differential equations.

References

↑ Polyanin, Andrei D.; Valentin F. Zaitsev (2003). Handbook of Exact Solutions for Ordinary Differential Equations, 2nd. Ed.. Chapman & Hall/CRC. ISBN 1-5848-8297-2.

Bibliography

A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition)", Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2
A. D. Polyanin, V. F. Zaitsev, and A. Moussiaux, Handbook of First Order Partial Differential Equations, Taylor & Francis, London, 2002. ISBN 0-415-27267-X
D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.
Hartman, Philip, Ordinary Differential Equations, 2nd Ed., Society for Industrial & Applied Math, 2002. ISBN 0-89871-510-5.
W. Johnson, A Treatise on Ordinary and Partial Differential Equations, John Wiley and Sons, 1913, in University of Michigan Historical Math Collection
E.L. Ince, Ordinary Differential Equations, Dover Publications, 1958, ISBN 0486603490
Witold Hurewicz, Lectures on Ordinary Differential Equations, Dover Publications, ISBN 0-486-49510-8

External links

Differential Equations at the Open Directory Project (includes a list of software for solving differential equations).
EqWorld: The World of Mathematical Equations, containing a list of ordinary differential equations with their solutions.
VisSim is a visual language for differential equation solving.
Online Notes / Differential Equations by Paul Dawkins, Lamar University.
Differential Equations, S.O.S. Mathematics.
A primer on analytical solution of differential equations from the Holistic Numerical Methods Institute, University of South Florida.
Mathematical Assistant on Web online solving first order (linear and with separated variables) and second order linear differential equations (with constant coefficients), including intermediate steps in the solution.
Ordinary Differential Equations and Dynamical Systems lecture notes by Gerald Teschl.
Notes on Diffy Qs: Differential Equations for Engineers An introductory textbook on differential equations by Jiri Lebl of UIUC.
DotNumerics: Ordinary Differential Equations for C# and VB.NET Initial-value problem for nonstiff and stiff ordinary differential equations (explicit Runge-Kutta, implicit Runge-Kutta, Gear’s BDF and Adams-Moulton).
Online experiments with JSXGraph

Ordinary differential equation

Contents

Existence and uniqueness of solutions

Definitions

Ordinary differential equation

Solutions

Examples

Reduction to a first order system

Linear ordinary differential equations

Homogeneous equations

Nonhomogeneous equations

Fundamental systems for homogeneous equations with constant coefficients

Theories of ODEs

Singular solutions

Reduction to quadratures

Fuchsian theory

Lie's theory

Sturm–Liouville theory

References

See also

Bibliography

External links